Is meer altijd beter? We leven in een maatschappij waar we het liefst alles verbeteren: onze gezondheid, prestaties en ons plezier proberen we continue zo goed mogelijk te maken. Hierbij gaan we, wellicht gedreven door gemakszucht, wellicht door onwetendheid, meestal uit van lineaire verbanden. Want: meer van het ene leidt automatisch tot meer van het andere! Toch?
Lineaire verbanden zijn makkelijk te begrijpen. Voor het gemak gaan we er daarom vaak maar van uit dat de wereld om ons heen lineair is, een aanname die wordt gevoed door wetenschappelijke principes. Zie de grafiek hiernaast: een duidelijke lineaire relatie, je kan er makkelijk een rechte lijn doorheen trekken. Maar als er in deze grafiek een paar punten zouden wegvallen, dan is het al een stuk moeilijker om de lineaire relatie vast te stellen. Deze "gemakszucht" als het gaat om het onbewust stellen van lineaire verbanden wordt in de wetenschap daarnaast versterkt door "Ockhams scheermes", een theorie van Wilhelm van Ockham. Deze theorie stelt dat we bij het bepalen van onderlinge verbanden tussen elementen die in de wereld voorkomen altijd de simpelste benadering, namelijk degene met de minste aannames, moeten kiezen.
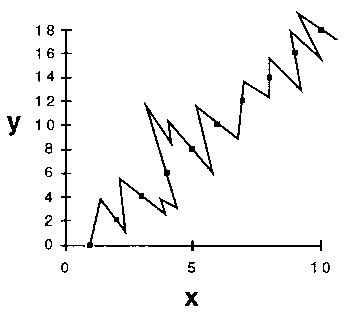 In de grafieken links en rechts is deze theorie geïllustreerd. De punten in de grafiek kunnen worden verbonden met een rechte lijn (links), of een lijn die alle kanten op schiet (rechts). Ockhams scheermes zegt dat we in dit soort gevallen altijd de linker mogelijkheid moeten kiezen, gezien deze op de minste
In de grafieken links en rechts is deze theorie geïllustreerd. De punten in de grafiek kunnen worden verbonden met een rechte lijn (links), of een lijn die alle kanten op schiet (rechts). Ockhams scheermes zegt dat we in dit soort gevallen altijd de linker mogelijkheid moeten kiezen, gezien deze op de minste
aannames berust.
Een voorbeeld van een vaak voorkomende relatie tussen biologische en psychologische factoren is de omgekeerde U-vorm, met de hoogste waarden voor y bij gemiddelde x-waarden. Als x erg groot wordt, gaat de waarde voor y juist weer omlaag. Een voorbeeld die dit goed laat zien is de Yerkes-Dodson wet, die de relatie tussen opwinding (in de vorm van stress) en prestaties op verschillende testen weergeeft. Deze wet laat zien dat een bepaalde mate van opwinding belangrijk is voor optimale cognitieve prestaties, maar dat teveel opwinding juist weer slecht is. Hierbij is juist middelmatigheid dus belangrijk voor de beste prestatie!
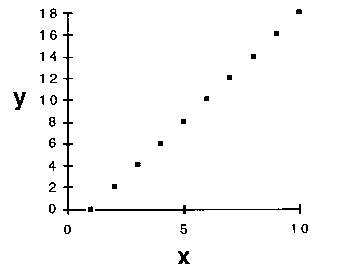 |
| Dit soort lineaire grafieken hebben we allemaal moeten tekenen bij wiskunde op de middelbare school. We gaan er vaak vanuit dat veel dingen in het leven een lineaire relatie hebben, maar is dit ook echt zo? (plaatje van http://www.hyle.org/journal/issues/3/hoffman.htm) |
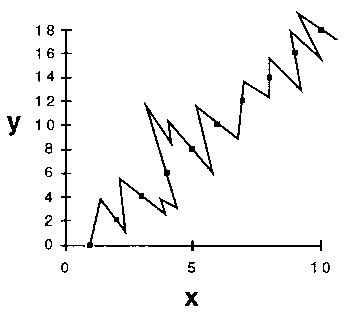 In de grafieken links en rechts is deze theorie geïllustreerd. De punten in de grafiek kunnen worden verbonden met een rechte lijn (links), of een lijn die alle kanten op schiet (rechts). Ockhams scheermes zegt dat we in dit soort gevallen altijd de linker mogelijkheid moeten kiezen, gezien deze op de minste
In de grafieken links en rechts is deze theorie geïllustreerd. De punten in de grafiek kunnen worden verbonden met een rechte lijn (links), of een lijn die alle kanten op schiet (rechts). Ockhams scheermes zegt dat we in dit soort gevallen altijd de linker mogelijkheid moeten kiezen, gezien deze op de minsteaannames berust.
Lineaire wereld?
Mede door dit principe zijn we dus geneigd veel verbanden in de onzekere wereld in ons heen zo simpel mogelijk te verklaren en dit is vaak goed, omdat het geen overmoedige conclusies in de hand werkt. Echter, niet-lineaire verbanden blijken vaak aanwezig in onze wereld en veel van deze relaties worden niet herkend door de focus op makkelijkere, lineaire verbanden.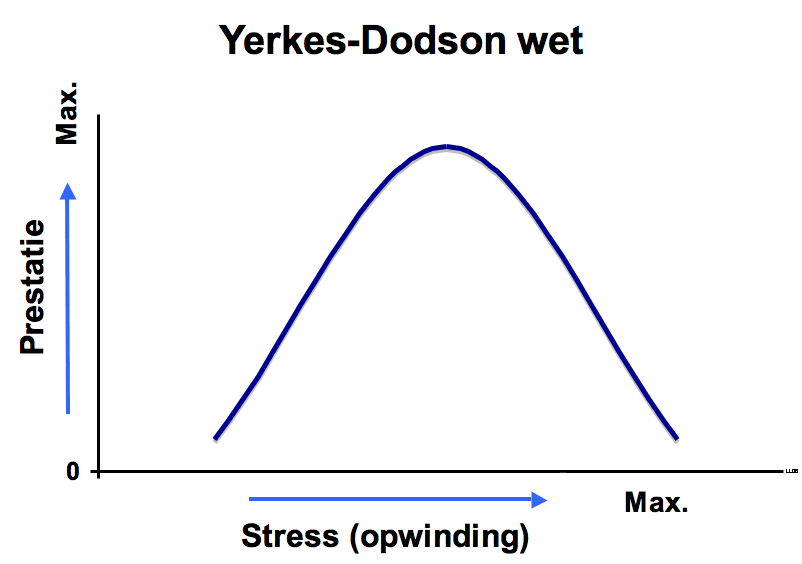 |
| De Yerkes-Dodson wet die de relatie tussen opwinding en prestatie beschrijft. (plaatje van http://commons.wikimedia.org/wiki/File:Yerkes-Dodson_wet.png) |
U-tjes in het dagelijkse leven
U-vorm verbanden zijn niet altijd even makkelijk vast te stellen, meestal omdat er niet altijd genoeg punten gemeten (kunnen) worden. Daarnaast zijn lineaire verbanden gewoon makkelijker te testen. We weten dus niet hoeveel verbanden in onze wereld zo'n omgekeerde U-vorm volgen. Als ik een gok zou mogen doen zou ik verwachten dat veel verbanden die wij nu als lineair beschouwen eigenlijk een andere vorm hebben. Middelmatigheid is bij deze omgekeerde U-verbanden dus goed: niet teveel en niet te weinig is het sleutelwoord. Een te grote toename van het één (hierboven stress) kan zelfs desastreus zijn voor het ander (prestatie op een taak), waardoor het stimuleren van deze ene factor niet altijd de juiste keus is. Denk hierbij bijvoorbeeld aan het gebruik van Ritalin of caffeïne voor het verbeteren van je aandachtsspanne tijdens het studeren: teveel is ook hier niet bevorderlijk. Het gezegde "doe maar gewoon dan doe je al gek genoeg" is misschien zo gek nog niet!
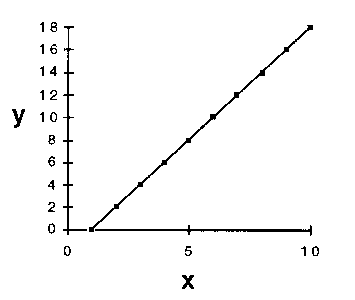
De rechter grafiek bij Ockhams scheermes is geen functie (meerdere mogelijke y-waarden bij een x-waarde). Is daar geen netter voorbeeld voor te vinden?
BeantwoordenVerwijderenNee dit is idd een overdreven voorbeeld van het principe, maar deze grafieken stonden bij elkaar op de genoemde website en leggen het idee volgens mij wel goed uit dus daarom heb ik voor deze gekozen. Als je een betere weet mag je 'm hier posten ;)
Verwijderen